パズルを通して人間の「思考」について考えてみる
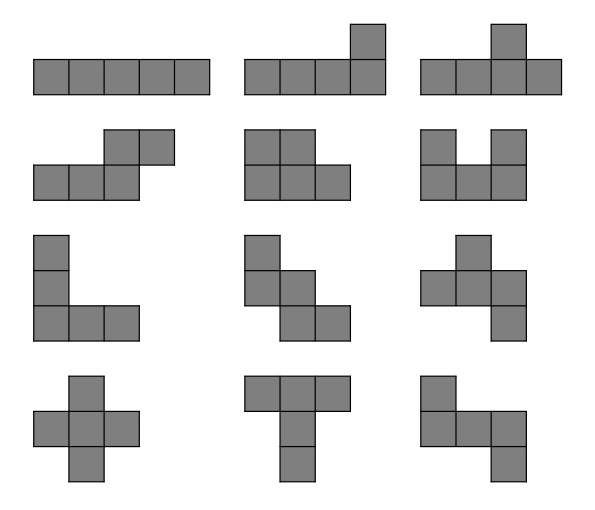
ペントミノ
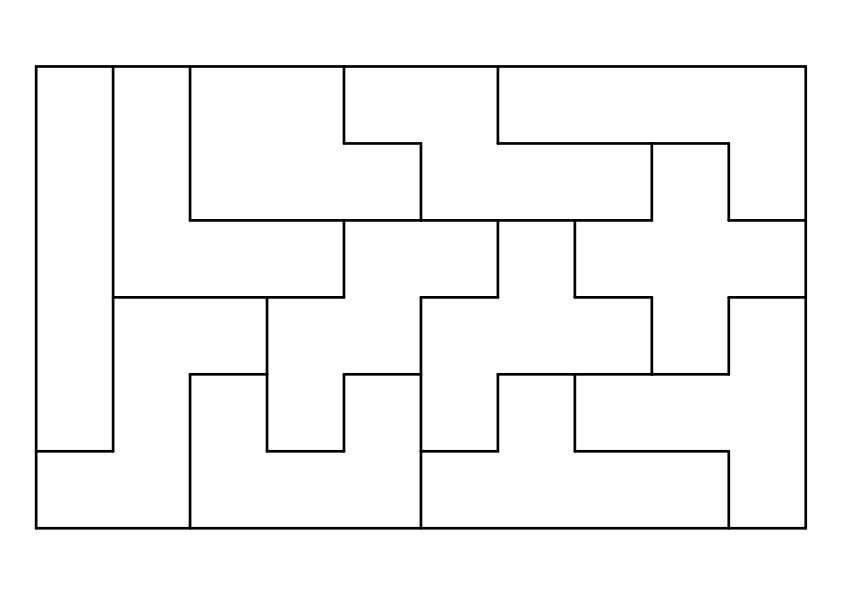
6✕10の長方形を作った例

立体版で3✕4✕5の直方体を作った例
「ペントミノパズル」というパズルをご存知でしょうか?
これは右の図(スマホの場合は下の図)のように五個の正方形を組み合わせてできる「ペントミノ」という12種類の図形を使ったパズルです。
12個の図形には合計で60個の正方形が含まれるので、これらを使って6✕10の長方形であったり、5✕12の長方形を作るのがこのパズルの目的です。
下の写真は5個の立方体を使った「立体版」のペントミノで、これを使うと例えば3✕4✕5の直方体なども作ることも出来ます。
ちょっとした「頭の体操」になればと思い、写真のペントミノパズルを高校2年生のホームルームにおいています。
(ちなみにこのペントミノは数年前に生徒と作ったものです。製品は値段が高いのでホームセンターで売っている角材を切って接着して作りました。精度はいまいちですが十分使えます。)
このパズルの答えは一通りではなく長方形や直方体を作る組み合わせはかなりあります。
コンピューターを使って調べてみると6✕10の長方形を作る組み合わせは2339通り、5✕12の長方形は1080通り、3✕4✕5の直方体を作る組み合わせは3940通りも有るのです。
いずれも左右、上下を入れ替えたり180度回転した対称なものは同じものとした数字です。
初めて聞かれた方は組み合わせの多さに驚かれたのではないかと思います。
ちなみにコンピューターでこの解答を見つける方法は原理的には極めて単純なものです。
まず長方形のボード(プログラム上では2次元の配列)を用意して、その端から各ピースを一つづつ置いていき、その都度「他のピースと重ならないか」「ボードの外にはみ出さないか」をチェックします。もし重なったりはみ出したら、回転したものを試し、それでもだめなら別のピースでやり直します。これを続けていって最終的にボードを埋め尽くすことができれば正解です。
このように高度なテクニックや論理を使うのではなく、コンピューターの処理速度の速さにまかせて、あらゆる可能性を「しらみつぶし」に調べ上げるのです。
こんなに解答が有るのだったら人間がやってもすぐに見つかりそうなものですが、実際にやってみるとこのパズルは結構手強いことがわかります。もっとも一般的な6✕10の長方形を作ろうとしても、結構時間がかかってしまうのではと思います。
ではどうすれば効率良く解答にたどり着けるのでしょうか?
それには「複雑すぎて最後までは読みきれないけど、その都度なるべく可能性が高そうな置き方をしていく」という方法が有効です。
これは右の図(スマホの場合は下の図)のように五個の正方形を組み合わせてできる「ペントミノ」という12種類の図形を使ったパズルです。
12個の図形には合計で60個の正方形が含まれるので、これらを使って6✕10の長方形であったり、5✕12の長方形を作るのがこのパズルの目的です。
下の写真は5個の立方体を使った「立体版」のペントミノで、これを使うと例えば3✕4✕5の直方体なども作ることも出来ます。
ちょっとした「頭の体操」になればと思い、写真のペントミノパズルを高校2年生のホームルームにおいています。
(ちなみにこのペントミノは数年前に生徒と作ったものです。製品は値段が高いのでホームセンターで売っている角材を切って接着して作りました。精度はいまいちですが十分使えます。)
このパズルの答えは一通りではなく長方形や直方体を作る組み合わせはかなりあります。
コンピューターを使って調べてみると6✕10の長方形を作る組み合わせは2339通り、5✕12の長方形は1080通り、3✕4✕5の直方体を作る組み合わせは3940通りも有るのです。
いずれも左右、上下を入れ替えたり180度回転した対称なものは同じものとした数字です。
初めて聞かれた方は組み合わせの多さに驚かれたのではないかと思います。
ちなみにコンピューターでこの解答を見つける方法は原理的には極めて単純なものです。
まず長方形のボード(プログラム上では2次元の配列)を用意して、その端から各ピースを一つづつ置いていき、その都度「他のピースと重ならないか」「ボードの外にはみ出さないか」をチェックします。もし重なったりはみ出したら、回転したものを試し、それでもだめなら別のピースでやり直します。これを続けていって最終的にボードを埋め尽くすことができれば正解です。
このように高度なテクニックや論理を使うのではなく、コンピューターの処理速度の速さにまかせて、あらゆる可能性を「しらみつぶし」に調べ上げるのです。
こんなに解答が有るのだったら人間がやってもすぐに見つかりそうなものですが、実際にやってみるとこのパズルは結構手強いことがわかります。もっとも一般的な6✕10の長方形を作ろうとしても、結構時間がかかってしまうのではと思います。
ではどうすれば効率良く解答にたどり着けるのでしょうか?
それには「複雑すぎて最後までは読みきれないけど、その都度なるべく可能性が高そうな置き方をしていく」という方法が有効です。

ペントミノ

6✕10の長方形を作った例

立体版で3✕4✕5の直方体を作った例
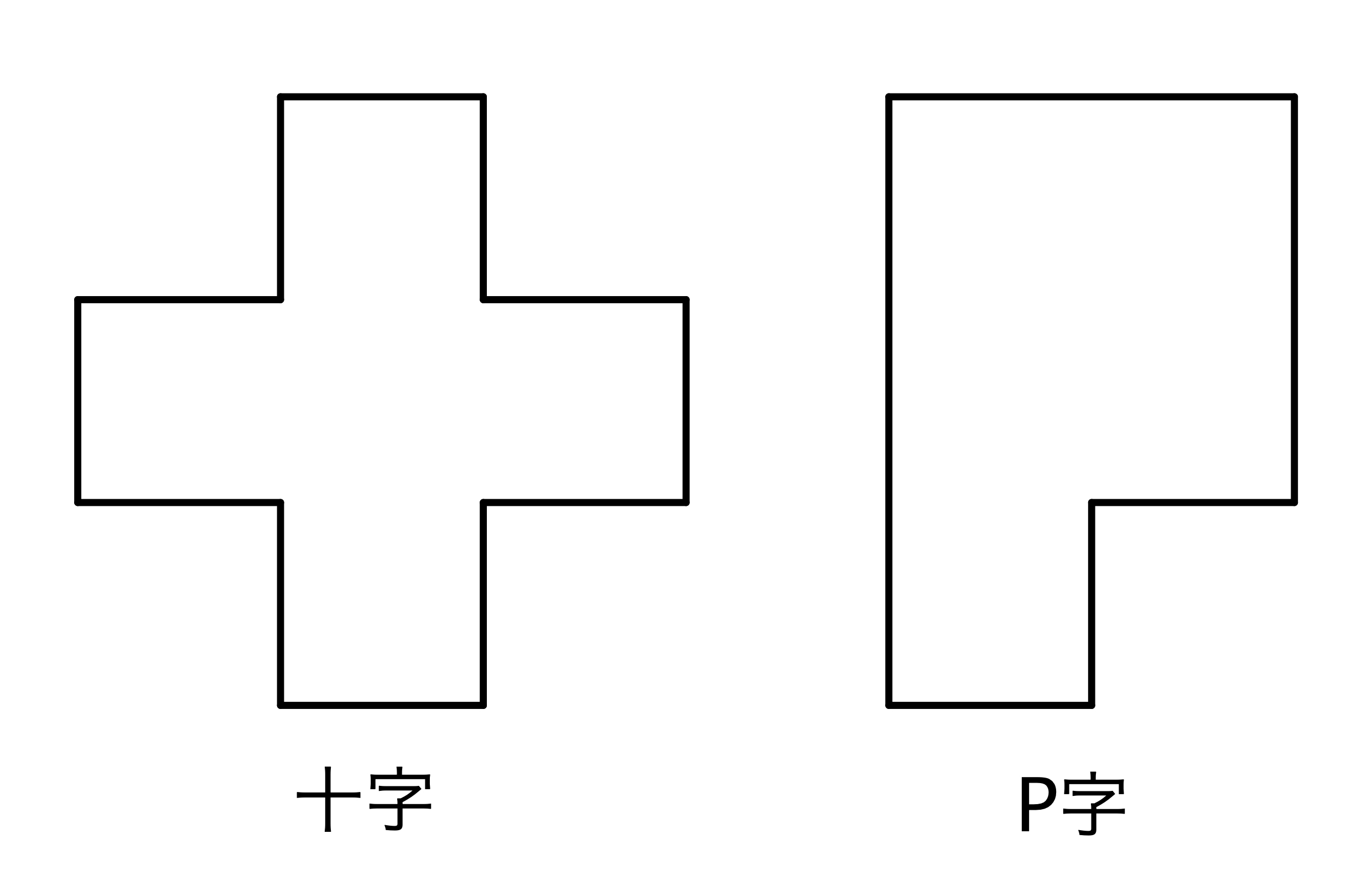
ちょっとわかりにくいと思うので、具体例で説明していきます。
例えば、右図の十字形をしたピースは四方が出っ張っていてとても「使いづらい」ピースです。何とんなく並べていって最後にこのピースがピッタリとハマるスペースが残る確率はかなり小さいと思います。ですから意識的にこのピースがハマるスペースを作り、早い段階で使ってしまえば「可能性」が広がります。
逆に右のP字と言われるピースは出っ張りが少なく「使いやすい」ので、これはなるべく「温存」しておくことも「可能性」を広げる方法です。
そして、一つひとつのピースを置いていく際には、「これを置いたら、次にはこっちが置けるかな」というように1手2手先を考えて、なるべく置けるピースが残るようにしていくのです。このようにすれば最後の方になっても置けるピースの自由度が維持され、たとえうまくいかなくても、最後の何ピースかを「組み替える」ことで正解にたどり着けたりするのです。
「最後までは見通せていないけど、その都度『可能性が高い』と感じる方向に進んでいく」といった作戦です。
これは処理能力に限界がある人間の脳にとっては「直感」を生かした効率的で有効な方法だと思います。
ただ、一方で「可能性が低い」と感じて切り捨ててしまったものの中にも正解が含まれていることがあります。実際、コンピューターの出した解答を見てみると、特に立体の場合など「こんな組み合わせがあったのか」と驚かされるものがあります。直感に頼らず「しらみつぶし」に調べなければとてもたどり着けそうもない複雑な解答があるのです。
今、コンピューターは囲碁や将棋の世界でもプロを凌駕する実力を付けています。
急速に実力が上がったのはディープラーニングという技術によるところが大きいようです。
これはコンピューターの処理速度を持ってしても解析しきれない複雑な現象に対しても「この状況ではこう対応すると結果が良くなる」ということを試行錯誤の中からコンピューターが学習していくことを可能にする技術です。「すべてを解析することは出来ないけど、その都度「良さそうな方向に進んでいく」という意味では、先程述べた人間の「直感」を生かした方法に近いものがあるように思います。
しかし「似ている」といってもコンピューターは人間に比べて圧倒的な処理速度を持ち、「変な思い込み」もないので、人間が「良くない手」と感じて切り捨ててしまったものの中にも、「良手」を見つけ出すことが可能です。これがコンピューターの強さの秘訣だろうと思います。
人間には見えてなかった部分をコンピューターが教えてくれたとも言えるでしょう。
このようにディープラーニングは画期的な技術ですが、成果を上げているのはルールが明確で数値化出来る一部の限られた世界だけです。そのへんの事情は以前の「雑感」で新井紀子さんの著書を紹介せせて頂いたときにお話しました。たぶん今後も、コンピューターが画期的な成果を上げる分野がある一方で、太刀打ちできない分野も残されていくし、その分野にも人間にとって未知の部分が膨大にあるのではと想像します。
そして、そうした分野ではやはり先述した「直感的方法」が重要な役割を担うと思います。
可能な限り論理的に考え、それでも先に進めない時は「直感的方法」に頼らざるを得ないからです。
そこでは間違った方向に進まないことが重要になりますが、あらかじめその正誤はわからないので、多数の試行錯誤、失敗の経験も含め、結果を絶えず検証して「直感」を磨いていくことが必要でしょう。
学習にもそうした視点を取り入れていくことが重要になると思います。
例えば、右図の十字形をしたピースは四方が出っ張っていてとても「使いづらい」ピースです。何とんなく並べていって最後にこのピースがピッタリとハマるスペースが残る確率はかなり小さいと思います。ですから意識的にこのピースがハマるスペースを作り、早い段階で使ってしまえば「可能性」が広がります。
逆に右のP字と言われるピースは出っ張りが少なく「使いやすい」ので、これはなるべく「温存」しておくことも「可能性」を広げる方法です。
そして、一つひとつのピースを置いていく際には、「これを置いたら、次にはこっちが置けるかな」というように1手2手先を考えて、なるべく置けるピースが残るようにしていくのです。このようにすれば最後の方になっても置けるピースの自由度が維持され、たとえうまくいかなくても、最後の何ピースかを「組み替える」ことで正解にたどり着けたりするのです。
「最後までは見通せていないけど、その都度『可能性が高い』と感じる方向に進んでいく」といった作戦です。
これは処理能力に限界がある人間の脳にとっては「直感」を生かした効率的で有効な方法だと思います。
ただ、一方で「可能性が低い」と感じて切り捨ててしまったものの中にも正解が含まれていることがあります。実際、コンピューターの出した解答を見てみると、特に立体の場合など「こんな組み合わせがあったのか」と驚かされるものがあります。直感に頼らず「しらみつぶし」に調べなければとてもたどり着けそうもない複雑な解答があるのです。
今、コンピューターは囲碁や将棋の世界でもプロを凌駕する実力を付けています。
急速に実力が上がったのはディープラーニングという技術によるところが大きいようです。
これはコンピューターの処理速度を持ってしても解析しきれない複雑な現象に対しても「この状況ではこう対応すると結果が良くなる」ということを試行錯誤の中からコンピューターが学習していくことを可能にする技術です。「すべてを解析することは出来ないけど、その都度「良さそうな方向に進んでいく」という意味では、先程述べた人間の「直感」を生かした方法に近いものがあるように思います。
しかし「似ている」といってもコンピューターは人間に比べて圧倒的な処理速度を持ち、「変な思い込み」もないので、人間が「良くない手」と感じて切り捨ててしまったものの中にも、「良手」を見つけ出すことが可能です。これがコンピューターの強さの秘訣だろうと思います。
人間には見えてなかった部分をコンピューターが教えてくれたとも言えるでしょう。
このようにディープラーニングは画期的な技術ですが、成果を上げているのはルールが明確で数値化出来る一部の限られた世界だけです。そのへんの事情は以前の「雑感」で新井紀子さんの著書を紹介せせて頂いたときにお話しました。たぶん今後も、コンピューターが画期的な成果を上げる分野がある一方で、太刀打ちできない分野も残されていくし、その分野にも人間にとって未知の部分が膨大にあるのではと想像します。
そして、そうした分野ではやはり先述した「直感的方法」が重要な役割を担うと思います。
可能な限り論理的に考え、それでも先に進めない時は「直感的方法」に頼らざるを得ないからです。
そこでは間違った方向に進まないことが重要になりますが、あらかじめその正誤はわからないので、多数の試行錯誤、失敗の経験も含め、結果を絶えず検証して「直感」を磨いていくことが必要でしょう。
学習にもそうした視点を取り入れていくことが重要になると思います。



