「かけ算の順序論争」をご存知でしょうか？
これは1972年のある報道をきっかけに始まり、今日まで50年以上にわたり議論が続けられている問題で、その概要は以下のとおりです。

ある小学校のテストで「6人のこどもに1人4個ずつミカンをあたえたい。ミカンはいくつあればよいでしょうか」という問題がだされました。何人かの子が答案に６✕４＝２４という式を書いたところ答えの２４個には丸をされたのですが、式の６✕４＝２４にはバツがされ、４✕６＝２４と訂正されたのです。
先生が訂正したのは、小学校ではかけ算の意味を
（1つあたりの数）✕（いくつ分）＝（全体の数）
と教えているので、答案もこの順番通りに
（一人あたりミカンの個数）✕（こどもの人数）＝　ミカンの総数　とすべきであると判断したからです。
この判断に疑問をもった親が当時の文部省に質問書をおくったことが新聞報道されると、これをきっかけに「かけ算に順序があるのか否か」をめぐって多くの人を巻き込んだ大論争がおきたのです。これが今も続く「かけ算の順序論争」です。

ちょっとネットで検索すればわかりますが、本当に多くの人がこの論争に参加し、様々な視点からの多種多様な意見が述べられてきました。しかし未だに統一的な見解が形成されることなく、議論が継続されているのです。そして残念ながら中には自分と反対の意見を持つ人を誹謗するような主張も散見されるのが現状です。

５０年の歳月がたち、意見も出し尽くされたであろう議論に今更参加する意味はあるのかという疑問もありますが、一介の数学教師としてこの問題に対する自分の考えを整理することは無意味ではないし、なにより生野学園では小学校から不登校している子もいて、実際にかけ算の意味を教える場面もあるので、自分はどう教えるのか？という実践的な意味もこめて少し考えてみようと思います。

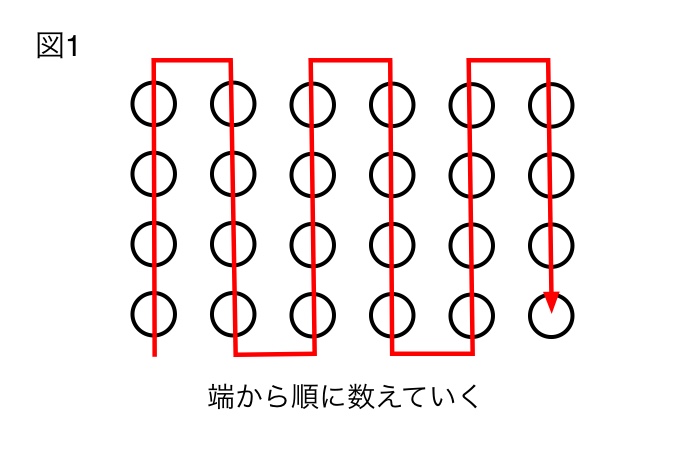
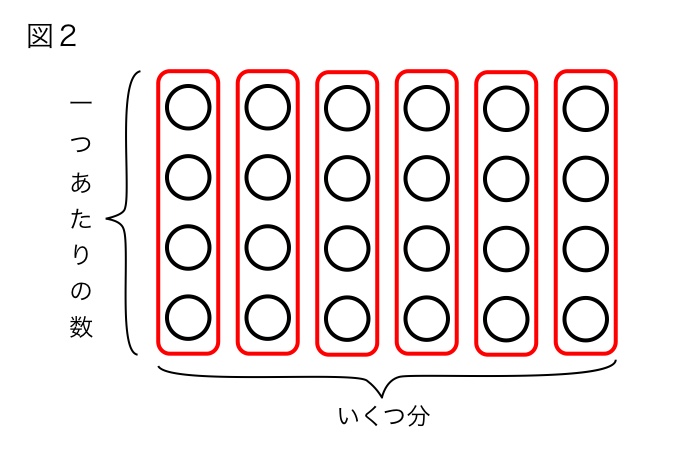
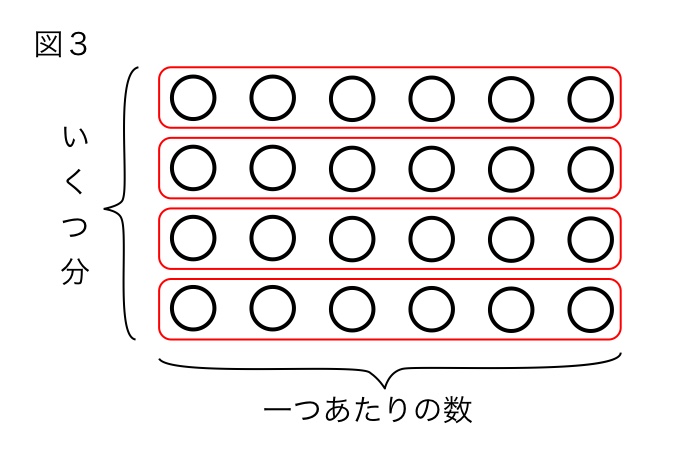
そして出来ればこの図のように縦横の２次元的なとらえ方ができるようになると良いと思います。なぜならこのように理解すれば図３のようにグループ分けを変えれば「4が6個でも、6が4個でも同じ」という「交換法則」に気づきやすいし、学年が上がって面積のような連続量を扱い、分数や小数のかけ算を考える際も移行しやすいからです。

何れにせよこの段階でかけ算の意味を理解するためには「１つあたりの数」と「いくつ分」の区別が出来るようになることが大切です。九九を暗記して計算が出来ても、この区別が出来ていなければ、かけ算の意味を理解したとは言えないのです。
また後に交換法則を理解すれば「区別しなくても同じ」ということに気づきますが、認識の順番として、それは区別が出来るようになった後で気付くことです。

次に「順序」の問題に入ります。
「１つあたりの数」と「いくつ分」を区別することが出来るようになったとして、それをどういう順番に書くのかということです。
日本の小学校で使われている教科書では
「１つあたりの数」✕「いくつ分」という順序で統一されています。しかしこれはかけ算の内在的な性質から導き出されたものではなく、ひとつの習慣にすぎません。
実際、国によっては逆に「いくつ分」✕「１つあたりの数」と書くのが習慣になっているところもあります。（これには使っている言語の語順が影響しているのかもしれません。）
いずれにせよ、これらはあくまで習慣であって、必ずそれに従わなければならないというものではありません。本来、順序はどちらでも良いのです。
そのため６✕４＝２４という式を見ただけではこの式を書いた人がどちらを「１つあたりの数」、どちらを「いくつ分」と考えて書いたのかは判別することは出来ません。

それにもかかわらず、どうしても順番から判別する必要があるのなら、例えば「『１つあたりの数』を先に、『いくつ分』を後に書く」ということを「約束」として導入する必要があります。そうすれば「約束」を受け入れた人たちの間では順序が意味を持つことになります。ただし、これは一般には通用しない「ローカルルール」であることを教える側はしっかり意識して伝えるべきだと思います。

ではこうした「ローカルルール」を導入するメリットは何でしょうか？
まず、かけ算の意味を理解する段階では「１つあたりの数を最初に書いてね」という約束をすることで２つの数の区別を意識付けする効果はあると思います。
また一人で多くの子どもたちを教えている学校の先生からすれば、式を見ただけである程度子どもたちの理解度を把握できるという利点はあるでしょう。
たぶん最初に挙げたミカンの問題であれば多くの子が４✕６＝２４という式を書くのではないかと思います。（もちろんこの中には「かけ算の意味がまだわかっていないけどたまたまこの順で書いた」という子も含まれているかもしれませんが、別の問題も何問かすればこうした「偶然性」は排除できるはずです。）そうすると、６✕４＝２４と書いた子どもにしぼって対応することができます。

ただし、６✕４＝２４と書いた理由はいくつか考えられるので注意が必要です。
まず考えられるのは、単純に問題文に出てきた数を順にかけたという可能性です。九九は暗記しているので答えは出せますが、まだ「１つあたりが何個で、それがいくつ分」というかけ算の考え方ができていない可能性があります。あるいはそもそも問題文をしっかり読まないで目についた数を順にかけたことも考えられます。こうした子どもたちにはとりわけ丁寧な対応が必要になると思います。

次に考えられるのは、かけ算の意味は理解できているけれど、どっちを先に書く約束だったかをわすれてしまった可能性です。この場合は生徒に図を描いてもらえばはっきりすると思います。あと、可能性は低いと思いますが「約束」に反発して意識的に逆順で書いたということもあるかもしれません。（小学生の頃の天邪鬼な自分ならやりかねなかったと思うので・・）

もう一つ考えられるのは「１つあたりの数」と「いくつ分」に対して別の考え方をした可能性です。
これは早くから指摘されていることですが、例えばミカンを６人に４個ずつ配るときに「トランプ配り方式」といって６人に１個ずつ配っていき、これを４回くり返すというやり方があります。このやり方であれば１回あたりが６個で、それが４回分なので「約束」通りに式を書いた場合は６✕４＝２４になるのです。

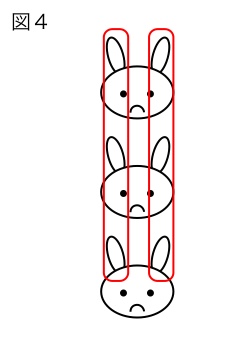
実はかけ算には交換法則が成り立つので、どんな問題であっても必ず２種類の考え方が出来ます。
例えば「ウサギが３匹います。耳はぜんぶでいくつでありますか？」という問題では、普通は「１匹あたり２つで、それが３匹分」と考えるのかもしれませんが、図４のように「片側に３つずつ、それが左右２つ分」というとらえ方も可能です。ですから３✕２＝６と書いたからと言って３本耳のウサギがいることにはならないのです。
たしかにこうした考え方をする子はめったにいないのかもしれません。でもその確認を怠ってはならないでしょう。

このように同じ６✕４＝２４という式を書いた場合でも様々なケースが考えられます。そのためローカルルールを導入するのであれば一人ひとりに「なぜそうしたか」を確認することは必須だと思います。本来テストは一人ひとりの理解度を知り、適切な対応をするために行うものですから、これは当たり前のことなのかもしれません。
以下、自分の考えをまとめておきます。

1. かけ算の学習では「１つあたりが何個で、それがいくつ分」という考え方が出来るようになることが大切である。
   
   
2. ただし、どちらを「１つあたりの数」とし、どちらを「いくつ分」とするかについては必ず２通りの考え方ができる。
   
   
3. 「１つあたりの数」と「いくつ分」を区別して式に書くとき、その順番はどちらでもかまわない。
   
   
4. それ故かけ算に順序があるように教えることは疑問である。
   
   
5. ただし「教えやすさ」「子どもたちの理解度の把握しやすさ」という理由で、ローカルルールであることを伝えた上で順序を約束することには一定の意味はある。
   
   
6. その場合であっても２で述べた理由から式の正誤を機械的に判断することは出来ず、一人ひとりに「なぜその順番で式を書いたのか」を丁寧に確認する必要がある。
   
   

最後に自分が教える場合にどうするかですが、幸い多人数の子どもたちに一斉に教えることはないのでローカルルールを導入する必要性は感じていません。